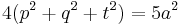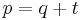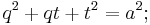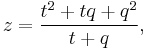Equilateral triangle

Equilateral triangle
An equilateral triangle is a regular polygon.
Family	2-simplex
Edges and vertices	3
Schläfli symbols	{3}
Coxeter–Dynkin diagrams
Symmetry group	Dihedral (D₃)
Internal angle (degrees)	60°

In geometry, an equilateral triangle is a triangle in which all three sides are equal. In traditional or Euclidean geometry, equilateral triangles are also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. They are regular polygons, and can therefore also be referred to as regular triangles.

1 Properties
2 Geometric construction
3 In culture and society
4 References
5 See also
6 External links

Properties

Assuming the lengths of the sides of the equilateral triangle are 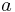$a\,\!$ , we can determine using the Pythagorean theorem that:

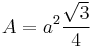
The area is $A=a^2\frac{\sqrt{3}}{4}$
The perimeter is $p=3a\,\!$
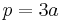
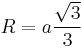
The radius of the circumscribed circle is $R=a\frac{\sqrt{3}}{3}$
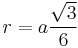
The radius of the inscribed circle is $r=a\frac{\sqrt{3}}{6}$
The geometric center of the triangle is the center of the circumscribed and inscribed circles
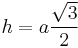And the altitude or height is $h=a\frac{\sqrt{3}}{2}$ .

For any point P in the plane, with distances p, q, and t from the vertices A, B, and C respectively,^[1]

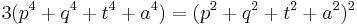$3(p^{4}+q^{4}+t^{4}+a^{4})=(p^{2}+q^{2}+t^{2}+a^{2})^{2}$ .

For any interior point P in an equilateral triangle, with distances d, e, and f from the sides, d+e+f = the altitude of the triangle, independent of the location of P.^[2]

For any point P on the inscribed circle of an equilateral triangle, with distances p, q, and t from the vertices,^[1]

$4(p^{2}+q^{2}+t^{2})=5a^{2}$

and

$16(p^{4}+q^{4}+t^{4})=11a^{4}$ .

For any point P on the minor arc BC of the circumcircle, with distances p, q, and t from A, B, and C respectively,^[1]

$p=q+t$

and

$q^{2}+qt+t^{2}=a^{2}�;$

moreover, if point D on side BC divides PA into segments PD and DA with DA having length z, then^[3]

$z= \frac{t^{2}+tq+q^2}{t+q},$

which also equals 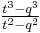$\tfrac{t^{3}-q^{3}}{t^{2}-q^{2}}$ if t ≠ q.

The triangle of largest area of all those inscribed in a given circle is equilateral; and the triangle of smallest area of all those circumscribed around a given circle is equilateral.^[4]

An equilateral triangle is the most symmetrical triangle, having 3 lines of reflection and rotational symmetry of order 3 about its center. Its symmetry group is the dihedral group of order 6 D₃.

A regular tetrahedron is made of four equilateral triangles.

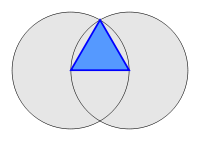
Equilateral triangles are found in many other geometric constructs. The intersection of circles whose centers are a radius width apart is a pair of equilateral arches, each of which can be inscribed with an equilateral triangle. They form faces of regular and uniform polyhedra. Three of the five Platonic solids are composed of equilateral triangles. In particular, the regular tetrahedron has four equilateral triangles for faces and can be considered the three dimensional analogue of the shape. The plane can be tiled using equilateral triangles giving the triangular tiling.

A result finding an equilateral triangle associated to any triangle is Morley's trisector theorem.

Geometric construction

Construction of equilateral triangle with compass and straightedge

An equilateral triangle is easily constructed using a compass. Draw a straight line, and place the point of the compass on one end of the line, and swing an arc from that point past halfway of the line segment. Repeat with the other side of the line. Finally, connect the point where the two arcs intersect with each end of the line segment

Alternate method:

Draw a circle with radius r, place the point of the compass on the circle and draw another circle with the same radius. The two circles will intersect in two points. An equilateral triangle can be constructed by taking the two centers of the circles and either of the points of intersection.

The proof that the resulting figure is an equilateral triangle is the first proposition in Book I of Euclid's Elements.

In culture and society

Equilateral triangles have frequently appeared in man made constructions:

Some archaeological sites have equilateral triangles as part of their construction, for example Lepenski Vir in Serbia.
The shape also occurs in modern architecture such as Randhurst Mall and the Jefferson National Expansion Memorial.
The Flag of the Philippines, the Seal of the President of the Philippines and the Flag of Junqueirópolis contain equilateral triangles.
The shape has been given mystical significance, as a representation of the trinity in The Two Babylons and forming part of the tetractys figure used by the Pythagoreans.
It is a shape of a variety of road signs, including the Yield sign.
Tau Kappa Epsilon a NIC Fraternity uses the Equilateral triangle as its primary symbol.

References

↑ ^1.0 ^1.1 ^1.2 De, Prithwijit, "Curious properties of the circumcircle and incircle of an equilateral triangle," Mathematical Spectrum 41(1), 2008-2009, 32-35.
↑ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, Dover Publ., 1996.
↑ Posamentier, Alfred S., and Salkind, Charles T., Challenging Problems in Geometry, second edition, Dover Publ. Co., 1996, pp. 170.
↑ Dorrie, Heinrich, 100 Great Problems of Elementary Mathematics, Dover Publ., 1965: 379-380.

External links

Weisstein, Eric W., "Equilateral Triangle" from MathWorld.